Articoli
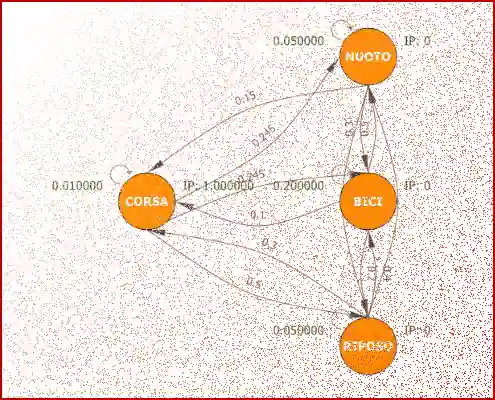
Nuovo all’analisi markoviana
L'analisi markoviana rappresenta una metodologia adatta a descrivere come sistemi o processi randomici si evolvono nel tempo. Questo metodo di modellazione viene anche chiamato "Catene di Markov"
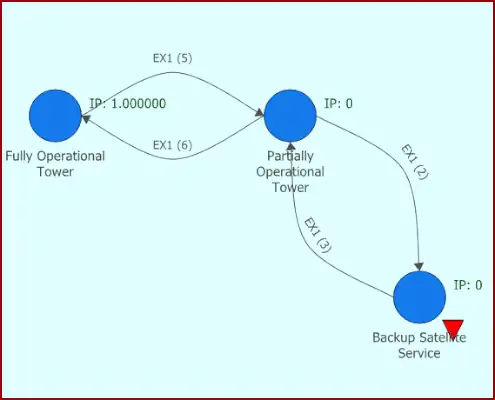
Analisi Markoviana
Le catene di Markov sono processi stocastici con la proprietà di Markov e modellizzano il comportamento di grandezze che variano nel tempo in modo randomico e con diversi andamenti. Furono inventate dal matematico russo Andrey Markov e forniscono un modello teorico per rappresentare l’evoluzione di un sistema a tempo discreto che

