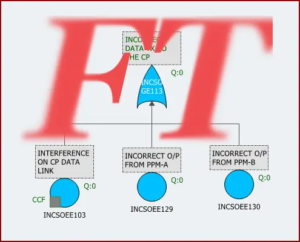
Articoli correlati
Analisi Markoviana
Le catene di Markov sono processi stocastici con la proprietà di Markov e modellizzano il comportamento di grandezze che variano nel tempo in modo randomico e con diversi andamenti. Furono inventate dal matematico russo Andrey Markov e forniscono un modello teorico per rappresentare l’evoluzione di un sistema a tempo discreto che può presentare ad ogni istante uno degli stati appartenente ad un insieme finito S={S1,…,Sn} e in cui la transizione da uno stato ad un altro avviene su base probabilistica.
Catene di Markov
Al variare dell’istante t il sistema “salta” da uno stato all’altro e la legge probabilistica secondo la quale avviene la transizione gode della proprietà di assenza di memoria nel senso che l’evoluzione delle probabilità future è determinata univocamente dalla conoscenza delle condizioni attuali della catena ( proprietà di Markov). In accezione semplice la markovianità consiste nell’asserire che la probabilità di essere in uno stato nell’istante t+1 dipende solamente dall’informazione che si ha nell’istante t e non dalla conoscenza che si ha degli istanti antecedenti. Quando si parla di probabilità e di stati si fa riferimento alle catene discrete mentre quando l’analisi si basa su tassi di transizione tra i vari stati si parla di catene continue.
In una catena di Markov discreta è necessario definire lo spazio degli stati che il sistema può assumere ad ogni istante temporale, S(t), e le rispettive probabilità di transizione ad ogni fase sia essa temporale che non. Il punto di partenza del modello è la determinazione di un vettore contenente le probabilità iniziali degli stati X(0) ={X1,…,Xn}, dove Xj è la probabilità all’istante t=0 che il sistema presenti lo stato j.
Una volta noto l’informazione circa una catena di Markov è interamente racchiusa nella matrice di transizione P, dove il generico elemento pij rappresenta la probabilità di passare dallo stato i allo stato j. P è chiamata matrice stocastica per le sue caratteristiche aleatorie dove P(i,j) è una matrice n x n p elementi nella quale la somma di ogni riga o ogni colonna è uguale a 1
Gli elementi della riga i-esima costituiscono le probabilità che la catena, trovandosi allo stato Si nell’istante t, transiti in S1, S2 o Sn all’istante successivo e, essendo tali eventi mutuamente esaustivi ed esclusivi, la somma degli elementi di ogni riga dovrà essere pari ad 1.
L’equazione di Chapman- Kolmogrov consente infine di calcolare la probabilità di presentare un certo stato dopo k step:
X(k) = X(0) Pk
Quindi la probabilità di mostrare uno stato ad un istante immediatamente successivo (t+1) si ottiene moltiplicando il vettore dello stato corrente (t) per P:
X(1) = X(0) P
Hanno un’ampia gamma di applicazioni tra cui l’analisi di sistemi riparabili e non riparabili e lo studio dei processi di degradazione: un semplice esempio è un sistema che può avere diversi livelli di funzionalità. Si consideri a tal punto l’operatività del pressostato di un compressore che può essere totale, parziale o nulla. Al tempo t=0 ha una funzionalità del 100% e ad ogni ciclo di utilizzo si hanno le probabilità di transizione mostrate in figura dalla quale si evince che il “salto” meno probabile è quello tra lo stato pienamente funzionante e quello di rottura al quale si associa una probabilità di accadimento pari a 0,001.
L’istante iniziale è configurato dal vettore X(0)=(1,0,0) e la matrice di transizione è
Una volta configurata la catena che rappresenta il sistema è possibile calcolare le probabilità puntuale e la probabilità media con la quale il compressore manifesta ciascuno dei tre stati in determinati cicli di utilizzo.
Ad esempio dopo 10 steps, seguendo la tabella dei risultati ottenuta con il software Blocksim, lo stato iniziale risulta quello più verosimile avendo una probsbilità del 91,7% mentre allo stato di rottura è associata una probabilità dello 0,8%.