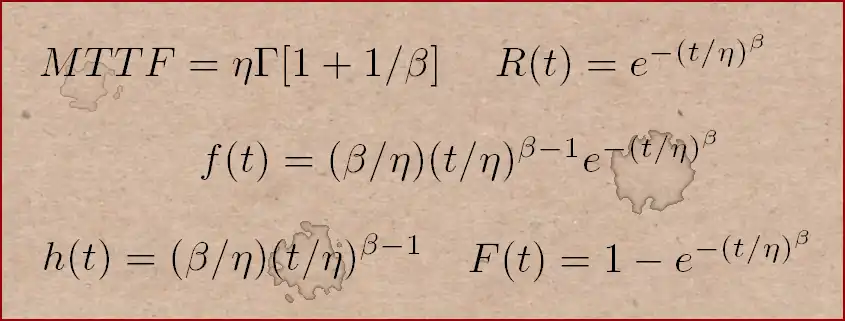Articoli correlati
Introduzione all’Analisi dei Dati di Vita Utile
L’analisi dei dati di vita utile (Reliability Life Data Analysis o più comunemente Weibull Analysis) si riferisce allo studio e modellazione dei dati di vita del prodotto osservato. Con il termine “dati di vita” si intende una particolare grandezza fisica che caratterizza la vita utile di un determinato oggetto. Ad esempio, i dati di vita possono essere misurati in:
- Ore di funzionamento (Run Hours)
- Chilometri percorsi
- Cicli di funzionamento e/o cicli al guasto
- Stress ciclici meccanici
- Stress ciclici termici
- …
Quando viene eseguita un’analisi dei dati di vita utile, d’ora in poi identificata con Weibull Analysis, l’analista cerca di effettuare una predizione sulla vita utile (quando si guasterà?) di tutti i prodotti su cui è effettuata l’analisi. Portando a guastarsi un numero molto ristretto di campioni rappresentativi, vengono poi interpolati in distribuzioni statistiche ed eseguite le previsioni.
Come verrà ripreso successivamente in questo articolo, uno degli aspetti più importati di questa tipologia di analisi è quella di migliorare la qualità dei test, riducendone i costi associati.
Distribuzioni di Vita Utile (Lifetime distribution)
Ingegneri, matematici e fisici hanno sviluppato nel tempo diversi modelli statistici per rappresentare i fenomeni naturali, non rappresentabile in modo deterministico. La funzione di densità di probabilità (Probabilistic Density Function o PDF) è una funzione matematica che descrive una distribuzione probabilistica di eventi. Nel caso dell’analisi dei dati di vita, due sono le funzioni maggiormente utilizzate:
- Log-Normale
- Weibull
Altre distribuzioni che possono essere utilizzate per modellare le distribuzioni di vita utile sono:
- Esponenziale
- Normale
- Gamma
- Gamma generalizzato
- Gumbel
- Mixed
- ….
Perché eseguire una analisi Weibull?
Waloddi Weibull inventò la distribuzione di Weibull nel 1937 e pubblicò i suoi risultati nel 1951, in America. Inizialmente valutata con scetticismo, fu sviluppata negli anni a venire ed oggi è ampiamente utilizzata in svariati settori, industriali e non, in quanto offre risultati realistici a fronte di un costo, in termini di denaro e tempo, inferiore rispetto ad altre distribuzioni.
Sebbene esistano altre tipologie di distribuzione, oggigiorno, quando si parla di analisi dei dati di vita si utilizzata il termine Weibull Analysis, in virtù del fatto che la distribuzione maggiormente utilizzata sia proprio quella di Weibull.
La formulazione della PDF di Weibull più generale è composta da tre parametri (β, η, γ) ma in genere, per via di alcune limitazioni, si preferisce adottare una Weibull a due parametri, ponendo il parametro γ =0 ed in questo caso la pdf prende il nome di “Weibull a due parametri” o “semplicemente funzione Weibull”.
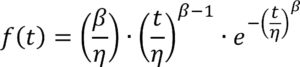
Funzione Weibull a due parametri
Tralasciando il terzo parametro gamma (γ), d’ora in poi non più considerato, il primo parametro beta (β), parametro di forma o pendenza, mostra la classe della modalità di guasto: mortalità infantile, random, usura inziale, o usura avanzata. Nella seguente figura vengono rappresentati le classi di guasto appena citate.
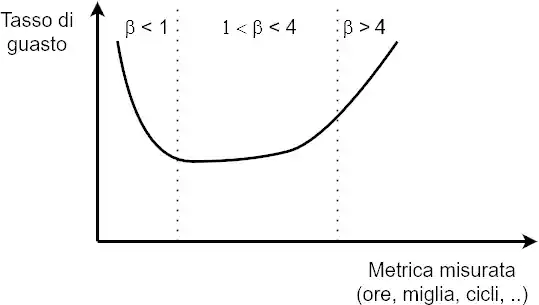
Curca a vasca da bagno (bathtub curve) tipica dei prodotti
Per β < 1 abbiamo un tasto di guasto molto elevato dovuto ai tipici problemi dei sistemi nuovi (rodaggio, utilizzo incorretto, …). Per β compreso tra 1 e 4, si parlerà di un tasso di guasto randomico (1) oppure di prima usura (>1). Quest’ultimo è quello di normale funzionamento nei normali sistemi fisici (si pensi ad una macchina). Con l’invecchiare del prodotto (chilometri percorsi, ore di funzionamento, cicli, …) il parametro b tenda ad aumentare di valore, dovuto ad un aumento del tasso di guasto. Infine, per β > 4 si inizierà a parlare di usura avanzata o rapida. In quest’ultima fase osserveremo un aumento repentino del numero di guasti del sistema.
Il secondo parametro eta (η), parametro di scala o vita caratteristica, è equivalente al tempo medio al guasto (MTTF) quando il parametro β = 1.
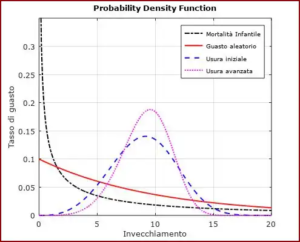
Nella seguente figura vengono riportate delle tipiche curve rappresentati diverse funzioni di densità di probabilità Weibull per diverse tipologie di prodotti. A fianco la loro rappresentazione del tasso di guasto.


Sospensioni e Guasti
In prima battuta possiamo definire quattro tipologie di dati nell’analisi Weibull, ossia il dato completo, censura destra, intervallato e censura sinistra. La prima tipologia è un dato di fatto, ossia un guasto osservato e segnalato. Le ultime tre tipologie invece sono il fulcro dell’analisi Weibull, in particolare la seconda tipologia, la censura destra, chiamata anche sospensione, introduce l’incertezza. Per avere un’idea dell’effetto delle sospensioni sul risultato finale, si consiglia l’articolo L’importanza delle sospensioni nel calcolo affidabilistico
L’incertezza è fondamentale in questo tipo di analisi, infatti se non avessimo incertezza, conseguenza diretta di aver portato a guastarsi tutto il campionario, non ci sarebbe bisogno di eseguire nessun tipo di analisi Weibull con un dispendio di costi e tempo non indifferente.
Questi e molti altri argomenti relativi alla tipologia dei dati, su come vanno trattati e quali benefici posso trarne, vengono affrontati esaustivamente nel corso ufficiale RSW250 Fundamentals of Reliability oppure al workshop Tecram WKS01 Ingegneria dell’affidabilità.
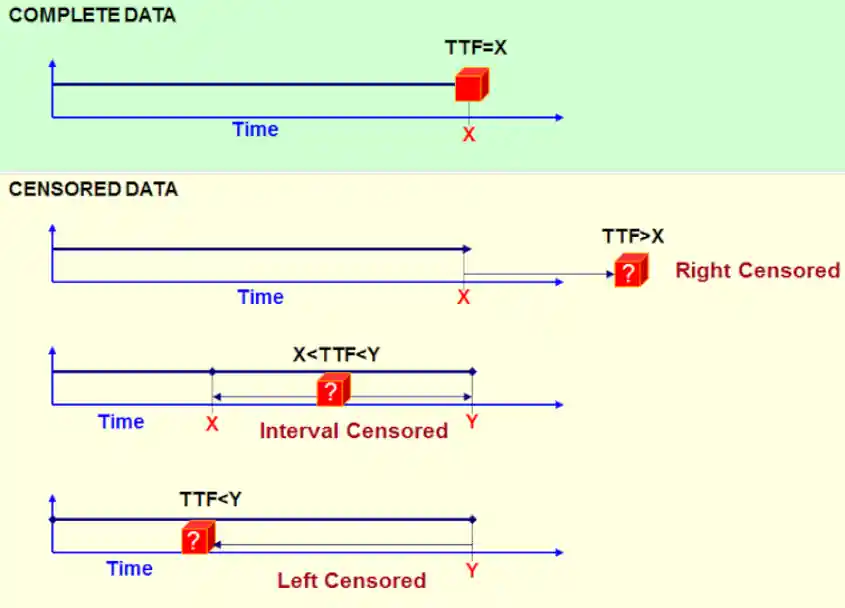
Tipologie di dati affidabilistici. Dalla prima in alto, dati completi, sospensioni o censura destra, intervallari o sospensione sinistra.
Quando e perché effettuare una Weibull Analysis?
In primis, l’analisi Weibull si applica a prodotti non riparabili mentre per prodotti riparabili, la metodologia è diversa – vedasi l’articolo Nuovo all’ingegneria dell’affidabilità
Per poter meglio comprendere il campo di utilizzo, di seguito vengono riportate alcuni esempi di problemi ingegneristici risolti tramite l’analisi Weibull:
- A seguito di tre segnalazioni di guasto di un componente, il responsabile del progetto chiede:
- Quanti guasti avremo nel prossimo trimestre, semestre, anno?
- Quanto ci costerà?
- Qual è la miglior azione correttiva da intraprendere per ridurre o mitigare il rischio e le perdite?
- Per poter ordinare i pezzi di ricambio e programmare la manodopera per la manutenzione, devo conoscere quante unità saranno restituite nei prossimi mesi?.
- Dopo aver definito come guasto l’inquinamento del componente oltre una determinata soglia, individuare quando il mio sistema sarà oltre i termini previsti dalla legge.
- Dopo una modifica ingegneristica, quante unità devono essere testate per quanto tempo, senza alcun guasto, per verificare che la vecchia modalità di guasto sia stata eliminata o migliorata in modo significativo con un’affidabilità del 90%?
- un’azienda elettrica è afflitta da interruzioni dovute a guasti ai tubi del surriscaldatore. Sulla base di dati di ispezione limitati, si prevede la durata della caldaia in base all’ostruzione dei tubi guasti.
- l costo di un guasto non pianificato per un componente, soggetto a modalità di guasto per usura, è venti volte il costo di una sostituzione pianificata. Qual è l’intervallo di sostituzione ottimale?
- …
Riassumendo: è possibile valutare le tendenze, valutare la probabilità di funzionamento di un sistema in un intervallo di tempo, analizzare la vita media di un sistema, prevedere il tasso di guasti o persino determinare il periodo di garanzia.
Quali sono i vantaggi di un’analisi Weibull
Il vantaggio principale è quello di fornire una realistica e accurata analisi dei guasti e previsione dei guasti tramite l’utilizzo di un numero estremamente ridotto di campioni
- Si consideri il test di quattro cuscinetti meccanici. L’analisi Weibull è terminata alla rottura del primo campione, invece di portarli a rottura tutti.
Un altro fondamentale vantaggio è l’essere un metodo grafico utilizzabile sia dagli ingegneri che dai top manager riducendo al minimo il gap di comunicazione tipico tra direzione e reparto tecnico. La carta Weibull permette di leggere sui grafico il tasso di guasto e l’invecchiamento, la classe di guasto, il comportamento dei nuovi guasti e molto altro ancora.
Come eseguire l’analisi Weibull?
Tutte le analisi Weibull iniziano con il raccogliere ed organizzare i dati di vita utile del sistema analizzato. La raccolta dati è fondamentale per effettuare analisi Weibull accurate. Nel caso di risultati con livelli di confidenza inaccettabili potrebbe essere necessario ridefinire il metodo di raccolta dati. A tal riguardo si veda l’articolo sul processo FRACAS.
Una volta organizzati questi dati in un foglio di lavoro, si procede con la determinazione dei parametri caratteristici, attraverso metodi analitici o simulativi, tra cui:
- metodo della regressione lineare
- metodo del rank mediano
- metodo della massima verosimiglianza
- …
Ottenuti i parametri caratteristici si procede nel realizzare una serie di grafici con i quali viene analizzato e risolto il problema.
Oggigiorno questi tipi di analisi vengono eseguiti tramite software specifici come ReliaSoft Weibull++ in quanto permettono di ridurre al minimo la fase di inserimento ed organizzazione dei dati (fase fitta di errori umani) e di concentrarsi principalmente sullo studio e comprensione dei risultati.
ReliaSoft Weibull++
ReliaSoft Weibull++ mette a disposizione un completo set di strumenti per l’analisi dei dati di vita utile e di degradazione di un prodotto, sia esso riparabile o non. Un potente software sviluppato da ingegneri dell’affidabilità per gli ingegneri dell’affidabilità. Vanta un’interfaccia molto intuitiva per visualizzare rapidamente un problema osservandolo sotto diversi punti di vista. Un calcolatore che risponde a qualsiasi tipo di domanda sulle curve generate dall’analisi, una forte reportistica personalizzabile e molte funzionalità a supporto di un’indagine di natura affidabilistica.
Per maggiori informazioni sul software ReliaSoft Weibull++ potete contattarci al seguente link.
Il file .m contente il codice utilizzato per la realizzazione del grafico “Probability Density Function” in Octave è riportato di seguito ed è a libero utilizzo senza scopo di lucro. Si prega di contattarci per ulteriori informazioni.
Octave is free software licensed under the GNU General Public License (GPL).